【Deep Learning】What is regularisation ?

1. 什么是正则化

（以下来源于Gpt-4o mini）

正则化（Regularization）是一种用于防止模型过拟合（overfitting）的技术，主要应用于机器学习和统计建模中。过拟合发生在模型对训练数据的学习过于深入，以至于捕捉到数据中的噪声，而不仅仅是潜在的模式。这会导致模型在新数据上的表现不佳。

正则化的主要思想：

• 惩罚复杂模型：通过在损失函数中添加额外的惩罚项（正则项），来限制模型的复杂性。这使得模型在优化时不仅考虑预测准确性，还要考虑模型的复杂程度。

正则化的作用：

• 提高泛化能力：通过降低模型复杂度，使模型在新数据上的表现更为稳定。
• 特征选择：L1 正则化可以直接使一些特征的权重为零，从而进行特征选择。
• 控制过拟合：有效地防止模型学习到训练数据中的噪声，从而提升模型的预测能力。

2. 为什么要正则化

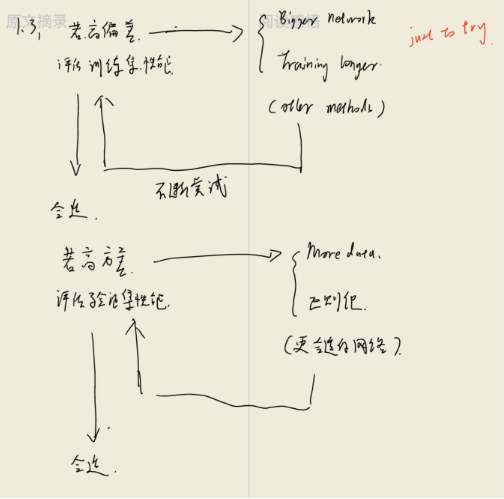
（我的笔记）

• 训练模型是一个漫长且反复的过程。在对数据集进行拟合检验时，通常会出现以下三种情况：overfitting、underfitting 和just right。分别对应拟合曲线高偏差、高方差和正合适的状态。

• 在高方差（过拟合）的过程中，前人总结了三种可行的办法：（1） 清洗数据（麻烦费时）; （2） 减少模型参数和大小，渐低复杂度; （3） 增加惩罚因子，也就是正则化。

• 对于回归模型和对应代价函数：

$$h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}^{2}+\theta_{3}x_{3}^{3}+\theta_{4}x_{4}^{4}$$

$$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2$$

• 一般来说，高次项使得模型在拟合过程中更加灵活，因此告高次项是导致方差偏大的直接原因。如果让这些高次项系数接近于零，就可以很好的改善模型过拟合的问题。

• 因此，我们对代价函数$J(\theta)$进行修改如下：

$$\operatorname*{min}_{\theta}J(\theta) = \operatorname*{min}_{\theta}\frac{1}{2m} \left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+1000\theta_{3}^{2}+10000\theta_{4}^{2}\right]$$

• 这里我们对方程增加了两个限制条件，分别对$\theta_3$和$\theta_4$进行限制，不让他们过高。

3. 如何对模型进行正则化

• 介绍三种常用方法：
  • $L_2$正则化
  • $L_1$正则化
  • Dropout

3.1 $L_2$参数正则化（Frobenius范数）

在其他学术圈，$L_2$也被称为岭回归或者Tikhonov正则。

• 方法：向目标函数添加一个正则项$\lambda \sum_{j=1}^{n} \theta_j^2$

$$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n} \theta_j^2$$

• 例如，对于logistic代价（吴恩达）

$$\mathrm{J~(w,b)=\frac1m~\sum_{i=1}^m~\left(\hat{y}^{(i)},y^{(i)}\right)}$$

• 可加入正则项，形成以下公式：

$$\mathrm{J~(w,b)=\frac1m~\sum_{i=1}^m~\left(\hat{y}^{(i)},y^{(i)}\right)}+\frac{\lambda}{2m}\left\|\boldsymbol{w}\right\|_2^2$$

• 因为$\left\|\boldsymbol{w}\right\|_2^2=W^TW$，所以也可以写成：

$$\mathrm{J~(w,b)=\frac1m~\sum_{i=1}^m~\left(\hat{y}^{(i)},y^{(i)}\right)}+\frac{\lambda}{2m}w^Tw$$

1. $\boldsymbol{w}$是模型中的权重参数向量（不包括偏置项），例如：$\boldsymbol{w} = [w_1, w_2, \dots, w_n]$。正则化项会对权重参数施加惩罚，以防止某些权重过大导致模型过拟合。通过惩罚权重的大小，模型会更偏向于让所有权重尽量小。

2. $\left\| \boldsymbol{w} \right\|_2^2$ 表示权重向量的 (L_2) 范数平方。数学上，(L_2) 范数的平方就是各权重的平方和：

   $$\left\| \boldsymbol{w} \right\|_2^2 = w_1^2 + w_2^2 + \cdots + w_n^2$$

   这一项的作用是对权重的大小进行约束。权重越大，损失函数中的正则化项就越大，因此优化时会倾向于使权重较小。通过对权重施加这个约束，可以减少模型的复杂度，使其更加平滑，避免模型对数据细节的过度拟合。

3. $\frac{\lambda}{2m}$是一个缩放因子，其中m是训练样本的数量。具体作用如下：

   $m$: 将正则化项的贡献除以训练样本的数量$m$，这一部分主要是为了标准化，使得正则化项的影响与样本数量成比例。这保证了无论训练样本数量多少，正则化项都能起到一致的作用。

   $\frac{\lambda}{2}$: 这一项的引入在对损失函数进行导数求解时可以简化计算，同时$\lambda$决定了正则化项对整体损失函数的影响程度

为什么$L_2$正则化会起作用：

• 由于在前向传播时，我们为代价函数添加了正则项$\Omega(\boldsymbol{\theta})=\frac{1}{2m}\left\|\boldsymbol{w}\right\|_2^2$，因此在后向传播时，我们也需要把这点考虑进去。

• $1-\frac{\alpha\lambda}{m}$肯定小于1，因此这就相当于进行了“权重衰减”。

3.2 $L_1$正则化

• 在线性回归中，$L_1$正则化被称为Lasso回归

  对模型参数$w$的$L_1$正则化被定义为：

  $$\Omega(\boldsymbol{\theta})=\left\|\boldsymbol{w}\right\|_1=\sum_i\left|w_i\right|$$

  也就是个参数绝对值之和。

• L1正则化可以使得参数稀疏化，即得到的参数是一个稀疏矩阵，可以用于特征选择

  • 稀疏性，说白了就是模型的很多参数是0。通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，很多参数是0，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，即使去掉对模型也没有什么影响，此时我们就可以只关注系数是非零值的特征。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。

• L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合。

• 还是看文章吧，比较难以理解，之后再补。深入理解L1、L2正则化open in new window

3.3 Dropout（随机失活）

• 黑匣子，很随机，常用于CV领域

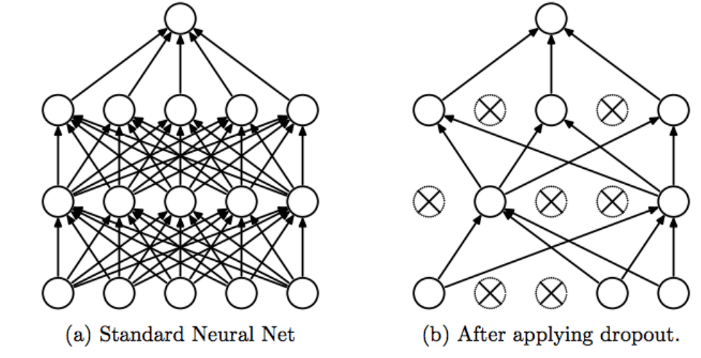
• 其主要思想就是在标准neural net中随机删去一些结点，让拟合曲线不再复杂。

  假设你在训练（a）图这样的神经网络，它存在过拟合，这就是dropout所要处理的，我们复制这个神经网络，dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5，设置完节点概率，我们会消除一些节点，然后删除掉从该节点进出的连线，最后得到一个节点更少，规模更小的网络（b），然后用backprop 方法进行训练。

• 实施dropout的常用方法——inverted dropout（反向随机失活）

  例如，在层数只有3的一个神经网络中，我们先生成$d^{[3]}$表示一个三层的dropout向量。

  d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep_prop
  

  并看其每一项是否都小于某数，称之为keep_prop，这是一个具体数字。如此，便为d3以keep_prop的概率生成了True和False的矩阵。

• 接下来用a3叉乘d3就可以得到最后经过dropout的a3。

  a3 = np.multipy(a3,d3)
  a3 /= keep_prop
  

  最后a3需要÷keep_prop保持期望值不变。

  它的功能是，不论keep-prop 的值是多少0.8，0.9 甚至是1，如果keep-prop 设置为1，那么就不存在dropout，因为它会保留所有节点。反向随机失活（inverted dropout）方法通过除以keep-prob，确保$𝑎^{[3]}$的期望值不变。

为什么drop-out会起作用？

• 直观上理解：不要依赖于任何一个特征，因为该单元的输入可能随时被清除，因此该单元通过这种方式传播下去，并为单元的四个输入增加一点权重，通过传播所有权重，dropout 将产生收缩权重的平方范数的效果，和之前讲的𝐿2正则化类似；实施dropout 的结果实它会压缩权重，并完成一些预防过拟合的外层正则化；𝐿2对不同权重的衰减是不同的，它取决于激活函数倍增的大小。
• 第二个直观认识是：我们从单个神经元入手。通过dropout，特殊单元的输入几乎被消除，有时这两个单元会被删除，有时会删除其它单元，就是说，一个特殊单元，它不能依靠任何特征，因为特征都有可能被随机清除，或者说该单元的输入也都可能被随机清除。我不愿意把所有赌注都放在一个节上，不愿意给任何一个输入加上太多权重，因为它可能会被删除，因此该单元将通过这种方式积极地传播开，并为单元的四个输入增加一点权重，通过传播所有权重，dropout 将产生收缩权重的平方范数的效果，和我们之前讲过的𝐿2正则化类似，实施dropout 的结果是它会压缩权重，并完成一些预防过拟合的外层正则化。
• 实施dropout 的另一个细节是：这是一个拥有三个输入特征的网络，其中一个要选择的参数是keep-prob，它代表每一层上保留单元的概率。所以不同层的keep-prob 也可以变化。第一层，矩阵𝑊[1]是7×3，第二个权重矩阵𝑊[2]是7×7，第三个权重矩阵𝑊[3]是3×7，以此类推，𝑊[2]是最大的权重矩阵，因为𝑊[2]拥有最大参数集，即7×7，为了预防矩阵的过拟合，对于这一层，我认为这是第二层，它的keep-prob 值应该相对较低，假设是0.5。对于其它层，过拟合的程度可能没那么严重，它们的keep-prob 值可能高一些，可能是0.7，这里是0.7。如果在某一层，我们不必担心其过拟合的问题，那么keep-prob 可以为1。

dropout的缺点。

• dropout 一大缺点就是代价函数𝐽不再被明确定义，每次迭代，都会随机移除一些节点，如果再三检查梯度下降的性能，实际上是很难进行复查的。定义明确的代价函数𝐽每次迭代后都会下降，因为我们所优化的代价函数J 实际上并没有明确定义，或者说在某种程度上很难计算，所以我们失去了调试工具来绘制这样的图片。我通常会关闭dropout 函数，将keep-prob 的值设为1，运行代码，确保𝐽函数单调递减。然后打开dropout 函数，希望在dropout 过程中，代码并未引入bug。

4. Conclusion

• 总结，解决训练模型过拟合问题最常用的办法就是正则化，正则化常用的有三种方法：$L_2$正则化；$L_1$正则化；和$Dropout$。

• 其中$L_2$正则化和$Dropout$的本质原理都是一样的，$L_1$正则化也有一定防止过拟合的功能，但更多用于参数稀疏化。

——《秒速五厘米》